Bourse & Matlab #9: Analyse de la volatilité des indices – Partie 3-3

La Bourse en Équation & Trading Algorithmique

Bourse & Matlab #9: Analyse de la volatilité des indices – Partie 3-3

Objectifs

Savoir analyser la volatilité d’un actif
Savoir effectuer une analyse comparative entre plusieurs actifs
Les erreurs à éviter durant son analyse
Savoir coder la volatilité d’un actif
Savoir calculer la variance et la variance mobile d’un actif
Comprendre la notion de la volatilité
Avoir l’importance de la volatilité
Savoir calculer la volatilité de type sinusoïdal ou Gaussien
Savoir la relation entre la volatilité et la valeur efficace
Savoir différencier entre la volatilité globale et mobile
Etc.

Téléchargement et importation des données

Dans cette on va aborder l’analyse de la volatilité d’un ensemble des indices. La première étape consiste le téléchargement et l’importation des données de cinq indices mondiaux : ‘CAC 40′,’FTSE 100′, ‘Nikkei 225′,’Dow Jones’ et ‘SP 500’ dans la BD Yahoo, ayant des symboles suivants successivement : ‘^FCHI’,’^FTSE’, ‘^N225′,’^DJI’,’^GSPC’. Ci-dessous l’extrait du code qui permet l’importation et l’affichage des données brutes du Jan-03-1995 à la date actuelle.

[pastacode lang=”c” manual=”%25%25%201.%20T%C3%A9l%C3%A9chargement%2C%20Importation%20%26%20Normalisation%20des%20donn%C3%A9es%0ATitre%3D%7B’%5EFCHI’%2C’%5EFTSE’%2C%20’%5EN225’%2C’%5EDJI’%2C’%5EGSPC’%7D%3B%0A%25%20%20%20%20%20%7B’CAC%2040’%2C’FTSE%20100’%2C%20’Nikkei%20225’%2C’Dow%20Jones’%2C’SP%20500’%7D%3B%0A%0A%25%20Titre%3D%7B’GBPUSD%3DX’%2C%20’EURUSD%3DX’%2C%20’JPY%3DX’%2C’CHF%3DX’%2C’NZDUSD%3DX’%7D%3B%0A%0AStart%3D’Jan-03-1995’%3B%20%20%20%20%25%20Date%20de%20d%C3%A9but%0AStop%3Ddatestr(now%2C1)%3B%20%20%20%20%25%20Date%20de%20fin%20(Actuelle)%20ou%20bien%20%22Mois-Jour-Ann%C3%A9e%22%0A%5Bnn%2C%20mm%5D%20%3D%20month(Stop)%3B%0AStop%3Dstrcat(mm%2C’-‘%2Cnum2str(day(Stop))%2C’-‘%2Cnum2str(year(Stop)))%3B%0A%0An%3Dlength(Titre)%3B%0AN%3D1e4%3B%0AData_H%3Dzeros(n%2CN)%3B%0AData_L%3Dzeros(n%2CN)%3B%0AMM%3D2*300%3B%20H%3Dones(1%2CMM)%2FMM%3B%20%25%20Filtre%20Moyenne%20Mobile%0A%0Afor%20i%3D1%3An%0A%20%20%20%20%25%20Importation%20%0A%20%20%20%20Data%20%3D%20getData(char(Titre(i))%2CStart%2CStop)%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20haut%20de%20la%20bougi%C3%A9%0A%20%20%20%20Data_H(i%2C%3A)%3Dimresize(Data(%3A%2C2)%2C%5BN%201%5D%2C’cubic’)%3B%0A%0A%20%20%20%20%25%20Prix%20bas%0A%20%20%20%20Data_L(i%2C%3A)%3Dimresize(Data(%3A%2C3)%2C%5BN%201%5D%2C’cubic’)%3B%0Aend%3B%0At%3Dlinspace(year(Start)%2Cyear(Stop)%2CN)%3B%0A%0A%25%20Affichage%0Afigure(1)%3B%0Aplot(t%2CData_H’%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0ATitre%3D%7B’CAC%2040’%2C’FTSE%20100’%2C%20’Nikkei%20225’%2C’Dow%20Jones’%2C’SP%20500’%7D%3B%0Alegend(Titre%2C’fontsize’%2C16%2C2)%3B%0Aset(gca%2C’color’%2C’none’)%3B” message=”” highlight=”” provider=”manual”/]

Assurez-vous bien que la date de du début soit supérieure à la date d’introduction en bourse de l’actif afin d’éviter les erreurs d’interprétation de son analyse.

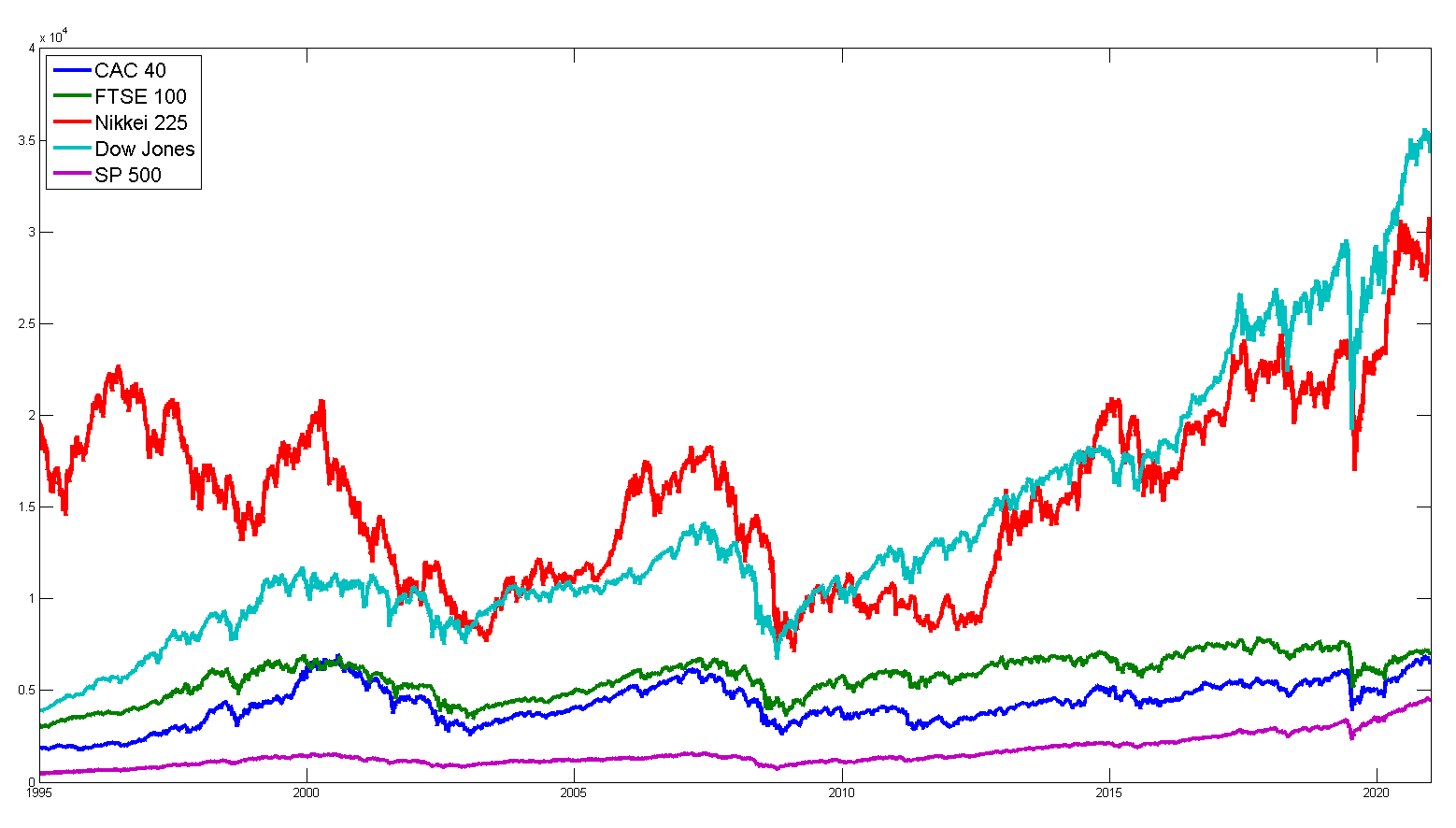
Données brutes des indices

On constate que les indices ‘Nikkei 225’ et ‘Dow Jones’ ont des amplitudes importantes par rapport aux autres indices. Une analyse comparative de la volatilité est difficile et illisible dans ces conditions. D’où l’importation de la normalisation des amplitudes.

A quoi sert la normalisation ?

La normalisation est une étape fondamentale durant son analyse des actifs du même type, en particulier lorsque ces derniers ont des amplitudes différentes. Elle consiste la normalisation des amplitudes des actifs pour quelle soient comprise entre [0 (0%), 1 (100%)]. En pratique, on divise le prix par la valeur maximale de la valeur absolue du prix dans la plage d’analyse (ici le prix le plus haut depuis 1995). On ajoute une ligne du code dans la boucle for :

[pastacode lang=”c” manual=”for%20i%3D1%3An%0A%20%20%20%20Data%20%3D%20getData(char(Titre(i))%2CStart%2CStop)%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20haut%20de%20la%20bougi%C3%A9%0A%20%20%20%20Data_H(i%2C%3A)%3Dimresize(Data(%3A%2C2)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_H(i%2C%3A)%3DData_H(i%2C%3A).%2Fmax(abs(Data_H(i%2C%3A)))%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20bas%0A%20%20%20%20Data_L(i%2C%3A)%3Dimresize(Data(%3A%2C3)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_L(i%2C%3A)%3DData_L(i%2C%3A).%2Fmax(abs(Data_L(i%2C%3A)))%3B%0Aend%3B%0A” message=”” highlight=”” provider=”manual”/]

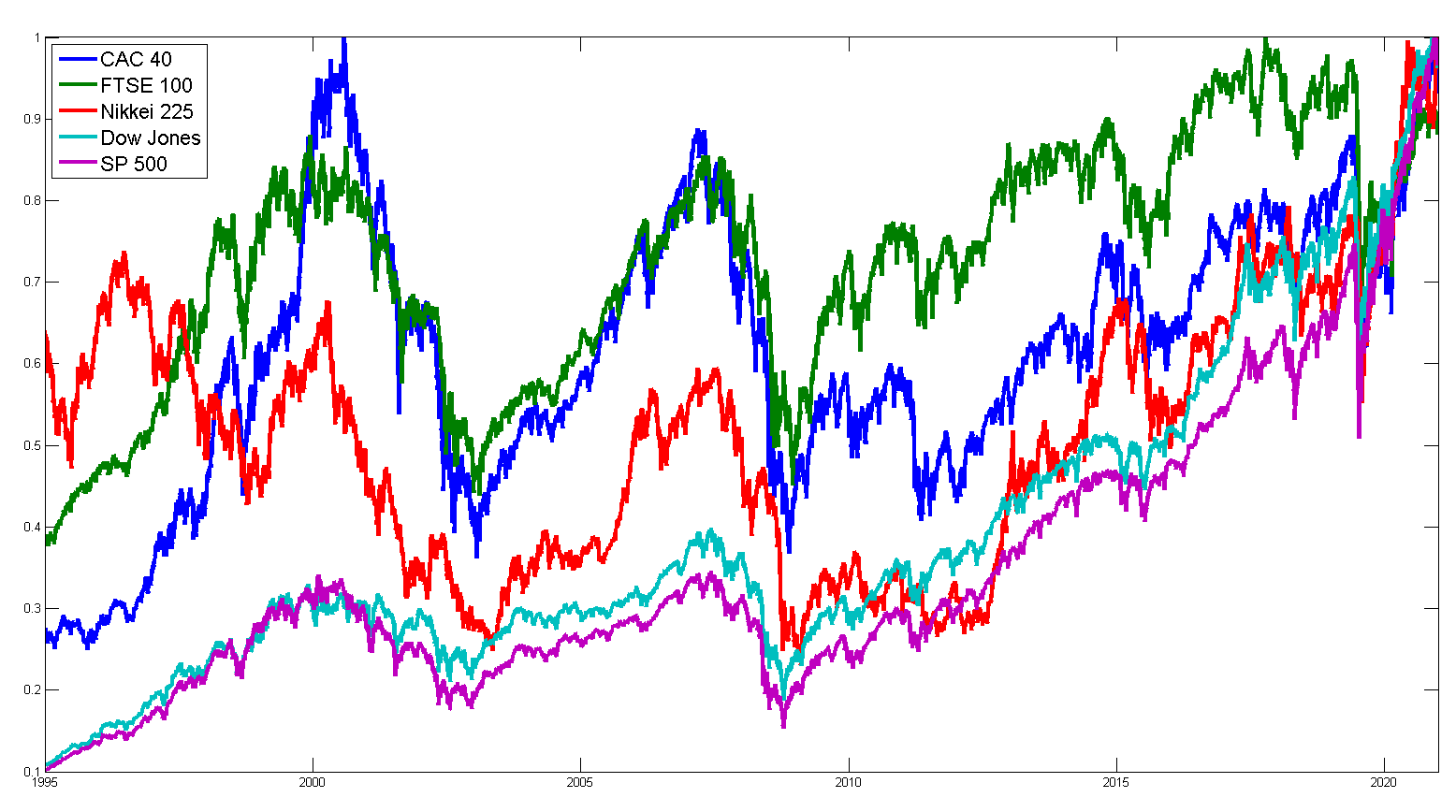
Données brutes des indices - normalisation des données

C’est mieux maintenant J On arrive à voir visuellement les la volatilité ainsi la ressemblance entre indices. On peut encore faire mieux, on normalise le point de départ des indices. En effet, les indices disposent des shifts différents (valeurs de départs différentes). On va soustraire la valeur initiale de la façon suivante :

[pastacode lang=”c” manual=”for%20i%3D1%3An%0A%20%20%20%20Data%20%3D%20getData(char(Titre(i))%2CStart%2CStop)%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20haut%20de%20la%20bougi%C3%A9%0A%20%20%20%20Data_H(i%2C%3A)%3Dimresize(Data(%3A%2C2)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_H(i%2C%3A)%3DData_H(i%2C%3A)-Data_H(i%2C1)%3B%0A%20%20%20%20Data_H(i%2C%3A)%3DData_H(i%2C%3A).%2Fmax(abs(Data_H(i%2C%3A)))%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20bas%0A%20%20%20%20Data_L(i%2C%3A)%3Dimresize(Data(%3A%2C3)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_L(i%2C%3A)%3DData_L(i%2C%3A)-Data_L(i%2C1)%3B%0A%20%20%20%20Data_L(i%2C%3A)%3DData_L(i%2C%3A).%2Fmax(abs(Data_L(i%2C%3A)))%3B%0Aend%3B” message=”” highlight=”” provider=”manual”/]

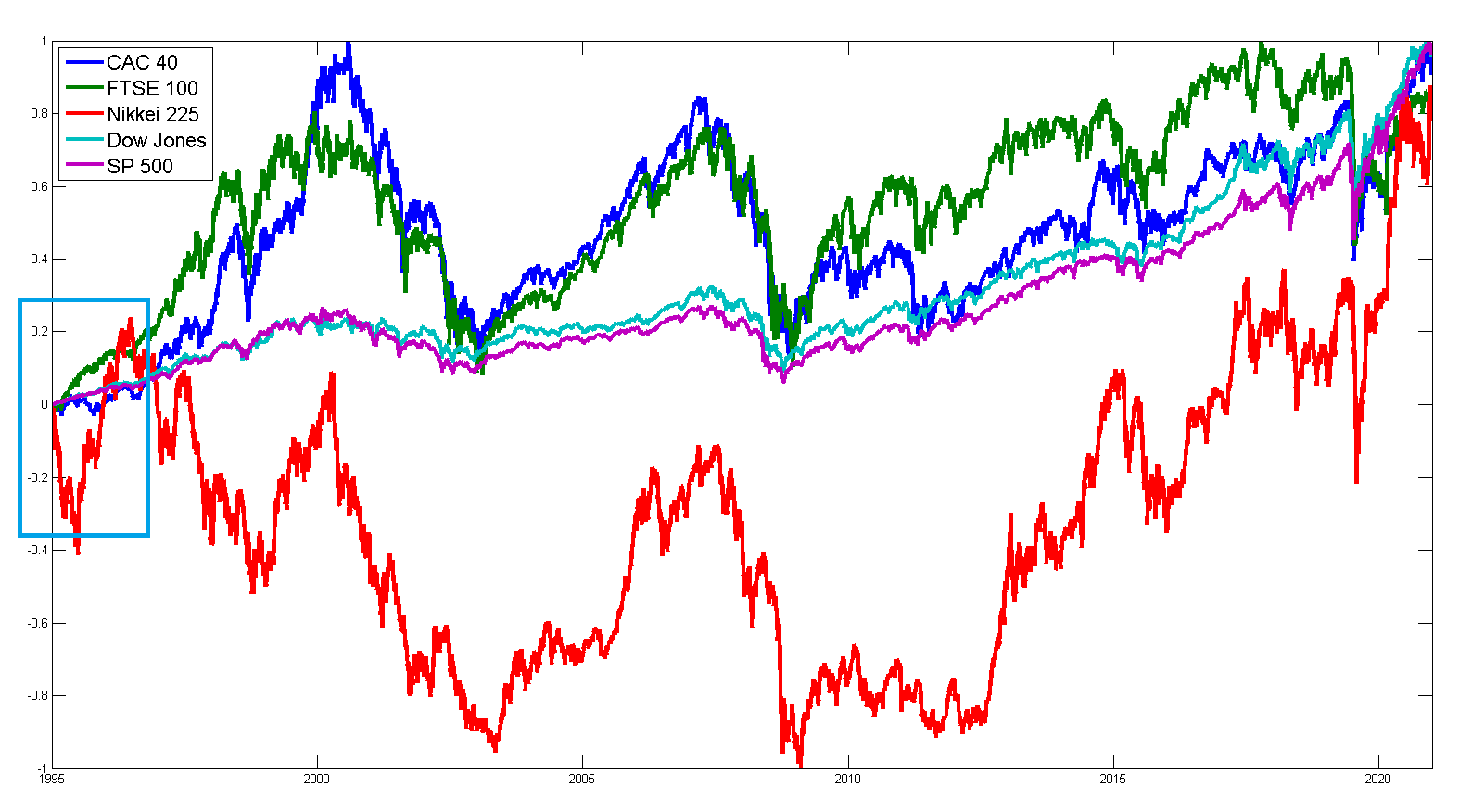
Données brutes des indices - normalisation des données et suppression offsets

Les données sont maintenant normalisées & alignées pour son analyse. Ci-dessous les points clés à retenir :

On constate une relation de corrélation entre [CAC 40 & FTSE 100] ainsi [S&P 500 & Dow Jones]
Pics durant les crises
Changement du comportement du CAC 40 & FTSE 100 depuis la crise du 2008
Nikkei 225 est l’indice la plus volatile, elle a un comportement unique ! (n’est pas corrélé aux autres indices)
S&P 500 & Dow Jones plus stables et robustes face aux crises
On est posé sur le pic comme celui du 2001 pour l’ensemble des indices 🙁

Voir le tutoriel pour plus de détails

Calcul de la volatilité globale en % (1 Sigma)

[pastacode lang=”c” manual=”Sig_H%3D100*sqrt(var(Data_H’))%3B%0ASig_B%3D100*sqrt(var(Data_L’))%3B%0Astrcat(num2str(Sig_H’)%2C’%20-%20’%2C%20char(Titre’))%0A” message=”” highlight=”” provider=”manual”/]

[pastacode lang=”c” manual=”ans%20%3D%0A%0A22.8422%20-CAC%2040%20%20%20%20%0A23.3533%20-FTSE%20100%20%20%0A%2039.359%20-Nikkei%20225%0A21.4884%20-Dow%20Jones%20%0A19.7517%20-SP%20500%20″ message=”” highlight=”” provider=”manual”/]

La volatilité à 1 Sigma du Nikkei 225 est 2x plus grande par rapport aux autres indices.

Calcul de la volatilité mobile

La volatilité mobile est un bon indicateur de la variabilité de la volatilité. En effet, la volatilité peut variée en fonction du temps comme la valeur moyenne. Elle indique la nervosité du marché ou sa stabilité. On peut aussi profiter de la volatilité mobile pour savoir les actifs corrélés. On voit clairement dans la figure une bonne corrélation (ressemblance) entre SP500 et DJ ainsi CAC40 et FTSE100. On verra dans la suite la notion de corrélation. Le nikkei225 lui en crise permanente 🙂

[pastacode lang=”c” manual=”M%3D150%3B%0ASig_M%3Dzeros(n%2CN)%3B%0Afor%20i%3D1%3An%0A%20%20%20%20for%20j%3DM%3AN%0A%20%20%20%20%20%20%20%20V%3DData_H(i%2Cj-M%2B1%3Aj)%3B%0A%20%20%20%20%20%20%20%20Sig_M(i%2Cj)%3Dsqrt(var(V))%3B%0A%20%20%20%20end%3B%0Aend%3B%0A%0Afigure(3)%3B%0Aplot(t%2C100*Sig_M’%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Alegend(Titre%2C’fontsize’%2C16%2C2)%3B%0Atitle(‘Volatilit%C3%A9%20(1%5Csigma)’%2C’fontsize’%2C16)%3B%0Aset(gca%2C’color’%2C’none’)%3B” message=”” highlight=”” provider=”manual”/]

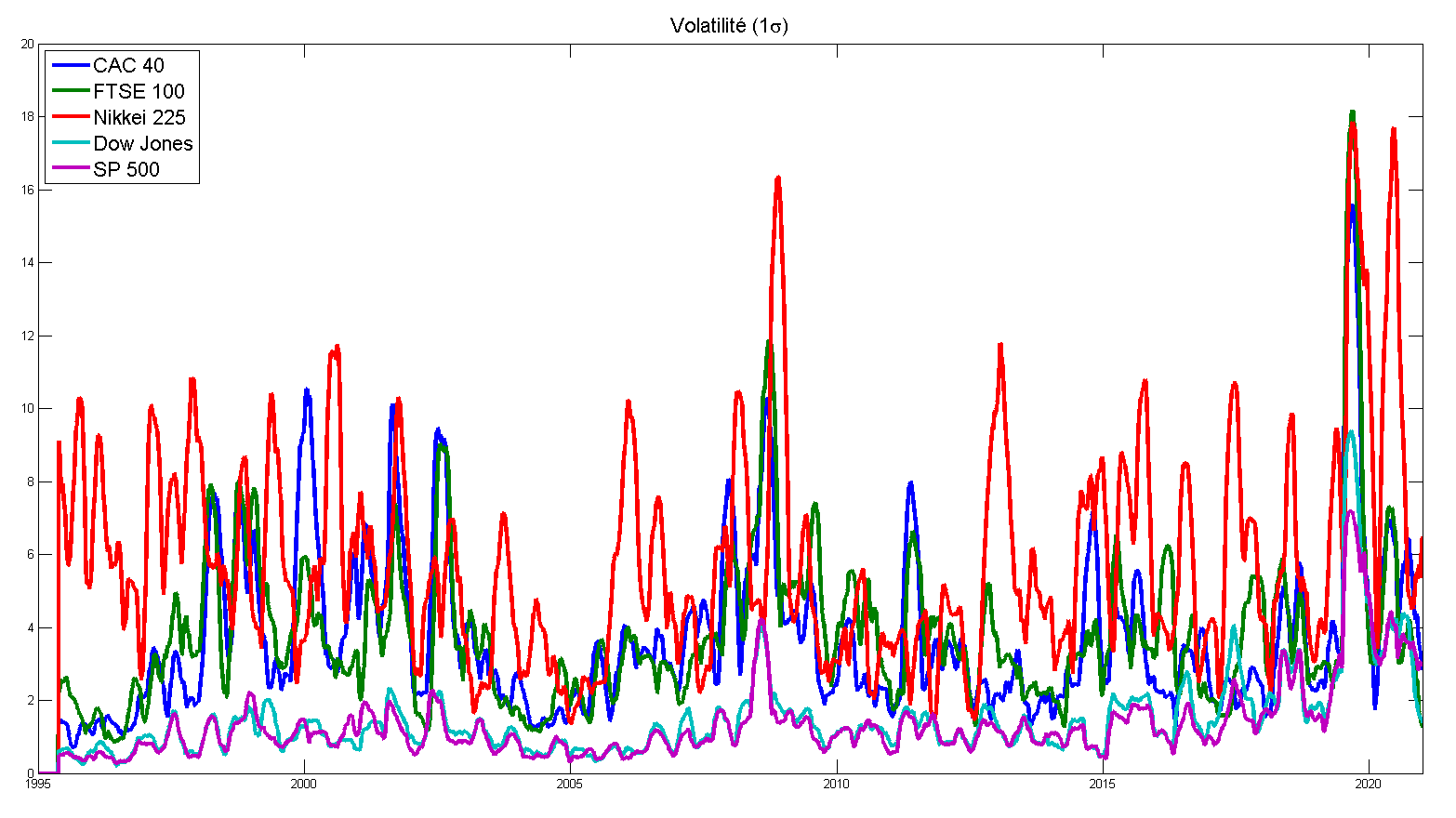
Volatilité mobile ou instantanée des indices

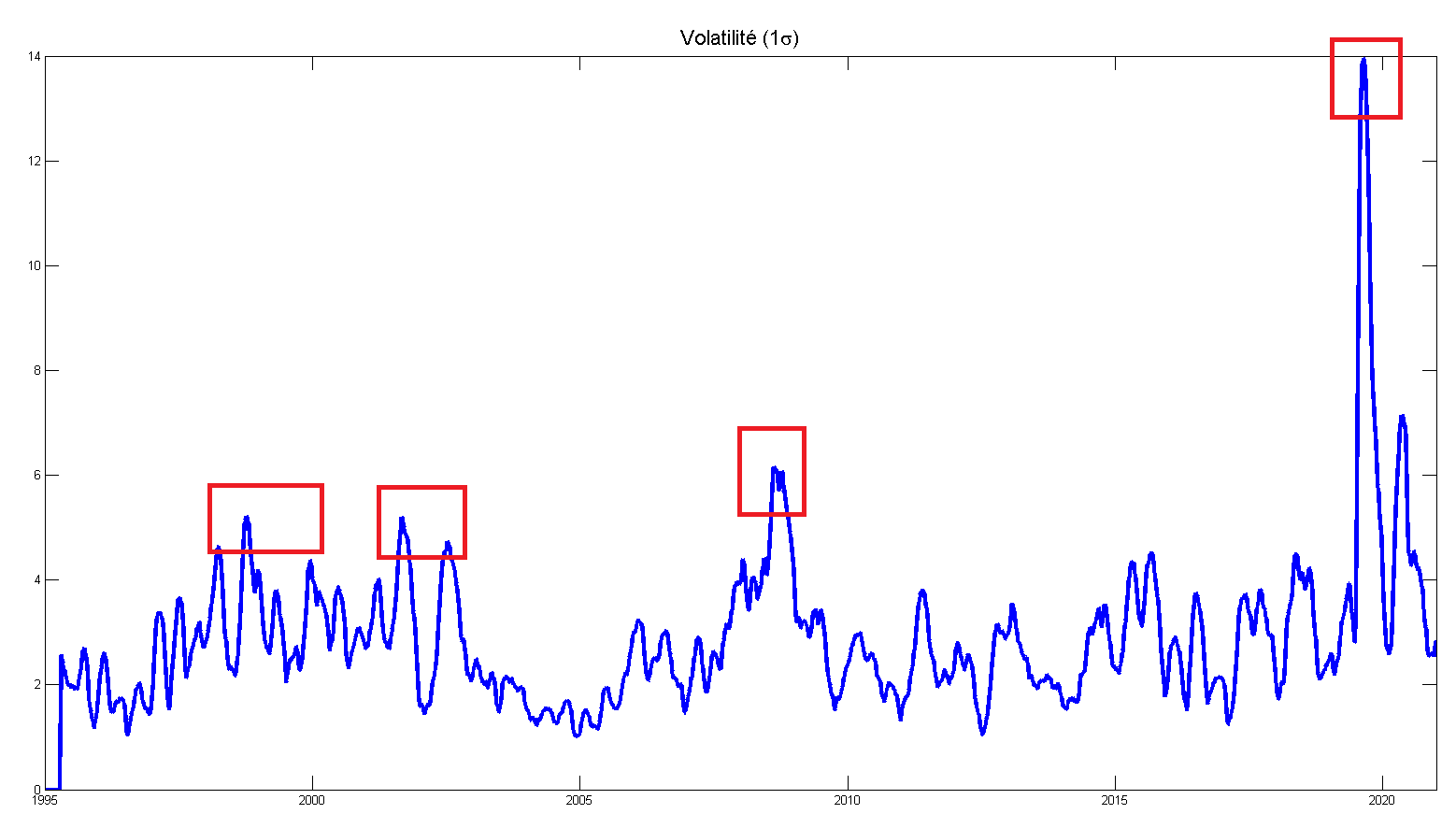
La volatilité mobile moyenne des indices

La crise COVID-19 est presque 2x plus volatile par rapport aux deux dernières crises.

[pastacode lang=”c” manual=”%25%25%203.%20Calcul%20de%20la%20Variance%20Mobile%0AM%3D120%3B%0ASig_M%3Dzeros(n%2CN)%3B%0Afor%20i%3D1%3An%0A%20%20%20%20for%20j%3DM%3AN%0A%20%20%20%20%20%20%20%20V%3DData_H(i%2Cj-M%2B1%3Aj)%3B%0A%20%20%20%20%20%20%20%20Sig_M(i%2Cj)%3Dsqrt(var(V))%3B%0A%20%20%20%20end%3B%0Aend%3B%0A%0Afigure(3)%3B%0Aplot(t%2C100*Sig_M’%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Alegend(Titre%2C’fontsize’%2C16%2C2)%3B%0Atitle(‘Volatilit%C3%A9%20(1%5Csigma)’%2C’fontsize’%2C16)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0A%0A%25%25%204.%20Calcul%20de%20la%20Variance%20Mobile%0AVM%3D100*sum(Sig_M)%2Fn%3B%0Afigure(4)%3B%0Aplot(t%2CVM%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Atitle(‘Volatilit%C3%A9%20(1%5Csigma)’%2C’fontsize’%2C16)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0A” message=”” highlight=”” provider=”manual”/]

Volatilité moyenne des indice

Programme complet

[pastacode lang=”c” manual=”clc%3B%20close%20all%3B%20clear%20all%3B%0A%0A%25%25%20Ingenierie-Bourse.fr%0A%25%25%20Comprendre%20la%20Volatilit%C3%A9%20-%20Partie%203%2F3%0A%0A%0A%25%25%201.%20T%C3%A9l%C3%A9chargement%2C%20Importation%20%26%20Normalisation%20des%20donn%C3%A9es%0ATitre%3D%7B’%5EFCHI’%2C’%5EFTSE’%2C%20’%5EN225’%2C’%5EDJI’%2C’%5EGSPC’%7D%3B%0A%25%20%20%20%20%20%7B’CAC%2040’%2C’FTSE%20100’%2C%20’Nikkei%20225’%2C’Dow%20Jones’%2C’SP%20500’%7D%3B%0A%0A%25%20Titre%3D%7B’GBPUSD%3DX’%2C%20’EURUSD%3DX’%2C%20’JPY%3DX’%2C’CHF%3DX’%2C’NZDUSD%3DX’%7D%3B%0A%0AStart%3D’Jan-03-1995’%3B%20%20%20%20%25%20Date%20de%20d%C3%A9but%0AStop%3Ddatestr(now%2C1)%3B%20%20%20%20%25%20Date%20de%20fin%20(Actuelle)%20ou%20bien%20%22Mois-Jour-Ann%C3%A9e%22%0A%5Bnn%2C%20mm%5D%20%3D%20month(Stop)%3B%0AStop%3Dstrcat(mm%2C’-‘%2Cnum2str(day(Stop))%2C’-‘%2Cnum2str(year(Stop)))%3B%0A%0An%3Dlength(Titre)%3B%0AN%3D1e4%3B%0AData_H%3Dzeros(n%2CN)%3B%0AData_L%3Dzeros(n%2CN)%3B%0AMM%3D2*300%3B%20H%3Dones(1%2CMM)%2FMM%3B%20%25%20Filtre%20Moyenne%20Mobile%0A%0Afor%20i%3D1%3An%0A%20%20%20%20Data%20%3D%20getData(char(Titre(i))%2CStart%2CStop)%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20haut%20de%20la%20bougi%C3%A9%0A%20%20%20%20Data_H(i%2C%3A)%3Dimresize(Data(%3A%2C2)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_H(i%2C%3A)%3DData_H(i%2C%3A)-Data_H(i%2C1)%3B%0A%20%20%20%20Data_H(i%2C%3A)%3DData_H(i%2C%3A).%2Fmax(abs(Data_H(i%2C%3A)))%3B%0A%20%20%20%20%0A%20%20%20%20%25%20Prix%20bas%0A%20%20%20%20Data_L(i%2C%3A)%3Dimresize(Data(%3A%2C3)%2C%5BN%201%5D%2C’cubic’)%3B%0A%20%20%20%20Data_L(i%2C%3A)%3DData_L(i%2C%3A)-Data_L(i%2C1)%3B%0A%20%20%20%20Data_L(i%2C%3A)%3DData_L(i%2C%3A).%2Fmax(abs(Data_L(i%2C%3A)))%3B%0Aend%3B%0At%3Dlinspace(year(Start)%2Cyear(Stop)%2CN)%3B%0A%0A%25%20Affichage%0Afigure(1)%3B%0Aplot(t%2CData_H’%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0ATitre%3D%7B’CAC%2040’%2C’FTSE%20100’%2C%20’Nikkei%20225’%2C’Dow%20Jones’%2C’SP%20500’%7D%3B%0Alegend(Titre%2C’fontsize’%2C16%2C2)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0A%0A%25%25%202.%20Calcul%20de%20la%20volatilit%C3%A9%20globale%0ASig_H%3D100*sqrt(var(Data_H’))%3B%0ASig_B%3D100*sqrt(var(Data_L’))%3B%0Astrcat(num2str(Sig_H’)%2C’%20-%20’%2C%20char(Titre’))%0A%0A%25%25%203.%20Calcul%20de%20la%20Variance%20Mobile%0AM%3D120%3B%0ASig_M%3Dzeros(n%2CN)%3B%0Afor%20i%3D1%3An%0A%20%20%20%20for%20j%3DM%3AN%0A%20%20%20%20%20%20%20%20V%3DData_H(i%2Cj-M%2B1%3Aj)%3B%0A%20%20%20%20%20%20%20%20Sig_M(i%2Cj)%3Dsqrt(var(V))%3B%0A%20%20%20%20end%3B%0Aend%3B%0A%0Afigure(2)%3B%0Aplot(t%2C100*Sig_M’%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Alegend(Titre%2C’fontsize’%2C16%2C2)%3B%0Atitle(‘Volatilit%C3%A9%20(1%5Csigma)’%2C’fontsize’%2C16)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0A%0A%25%25%204.%20Calcul%20de%20la%20Variance%20Mobile%0AVM%3D100*sum(Sig_M)%2Fn%3B%0Afigure(3)%3B%0Aplot(t%2CVM%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Atitle(‘Volatilit%C3%A9%20(1%5Csigma)’%2C’fontsize’%2C16)%3B%0Aset(gca%2C’color’%2C’none’)%3B” message=”” highlight=”” provider=”manual”/]

Laisser un commentaire Annuler la réponse

Vous devez vous connecter pour publier un commentaire.

Privacy & Cookie policy

Privacy & Cookies policy

Cookie name	Active

Qui sommes-nous ?

L’adresse de notre site Web est : https://ingenierie-bourse.fr.

Utilisation des données personnelles collectées

Commentaires

Quand vous laissez un commentaire sur notre site web, les données inscrites dans le formulaire de commentaire, mais aussi votre adresse IP et l’agent utilisateur de votre navigateur sont collectés pour nous aider à la détection des commentaires indésirables. Une chaîne anonymisée créée à partir de votre adresse de messagerie (également appelée hash) peut être envoyée au service Gravatar pour vérifier si vous utilisez ce dernier. Les clauses de confidentialité du service Gravatar sont disponibles ici : https://automattic.com/privacy/. Après validation de votre commentaire, votre photo de profil sera visible publiquement à coté de votre commentaire.

Médias

Si vous êtes un utilisateur ou une utilisatrice enregistré·e et que vous téléversez des images sur le site web, nous vous conseillons d’éviter de téléverser des images contenant des données EXIF de coordonnées GPS. Les visiteurs de votre site web peuvent télécharger et extraire des données de localisation depuis ces images.

Formulaires de contact

Cookies

Si vous déposez un commentaire sur notre site, il vous sera proposé d’enregistrer votre nom, adresse de messagerie et site web dans des cookies. C’est uniquement pour votre confort afin de ne pas avoir à saisir ces informations si vous déposez un autre commentaire plus tard. Ces cookies expirent au bout d’un an. Si vous vous rendez sur la page de connexion, un cookie temporaire sera créé afin de déterminer si votre navigateur accepte les cookies. Il ne contient pas de données personnelles et sera supprimé automatiquement à la fermeture de votre navigateur. Lorsque vous vous connecterez, nous mettrons en place un certain nombre de cookies pour enregistrer vos informations de connexion et vos préférences d’écran. La durée de vie d’un cookie de connexion est de deux jours, celle d’un cookie d’option d’écran est d’un an. Si vous cochez « Se souvenir de moi », votre cookie de connexion sera conservé pendant deux semaines. Si vous vous déconnectez de votre compte, le cookie de connexion sera effacé. En modifiant ou en publiant une publication, un cookie supplémentaire sera enregistré dans votre navigateur. Ce cookie ne comprend aucune donnée personnelle. Il indique simplement l’ID de la publication que vous venez de modifier. Il expire au bout d’un jour.

Contenu embarqué depuis d’autres sites

Les articles de ce site peuvent inclure des contenus intégrés (par exemple des vidéos, images, articles…). Le contenu intégré depuis d’autres sites se comporte de la même manière que si le visiteur se rendait sur cet autre site. Ces sites web pourraient collecter des données sur vous, utiliser des cookies, embarquer des outils de suivis tiers, suivre vos interactions avec ces contenus embarqués si vous disposez d’un compte connecté sur leur site web.

Statistiques et mesures d’audience

Utilisation et transmission de vos données personnelles

Durées de stockage de vos données

Si vous laissez un commentaire, le commentaire et ses métadonnées sont conservés indéfiniment. Cela permet de reconnaître et approuver automatiquement les commentaires suivants au lieu de les laisser dans la file de modération. Pour les utilisateurs et utilisatrices qui s’inscrivent sur notre site (si cela est possible), nous stockons également les données personnelles indiquées dans leur profil. Tous les utilisateurs et utilisatrices peuvent voir, modifier ou supprimer leurs informations personnelles à tout moment (à l’exception de leur nom d’utilisateur·ice). Les gestionnaires du site peuvent aussi voir et modifier ces informations.

Les droits que vous avez sur vos données

Si vous avez un compte ou si vous avez laissé des commentaires sur le site, vous pouvez demander à recevoir un fichier contenant toutes les données personnelles que nous possédons à votre sujet, incluant celles que vous nous avez fournies. Vous pouvez également demander la suppression des données personnelles vous concernant. Cela ne prend pas en compte les données stockées à des fins administratives, légales ou pour des raisons de sécurité.

Transmission de vos données personnelles

Les commentaires des visiteurs peuvent être vérifiés à l’aide d’un service automatisé de détection des commentaires indésirables.

Informations de contact

Informations supplémentaires

Comment nous protégeons vos données

Procédures mises en œuvre en cas de fuite de données

Les services tiers qui nous transmettent des données

Opérations de marketing automatisé et/ou de profilage réalisées à l’aide des données personnelles

Affichage des informations liées aux secteurs soumis à des régulations spécifiques

Save settings