N'hésitez pas de consulter notre chaîne YouTube "INGÉNIERIE et BOURSE" pour profiter des cours et tutos gratuits !

Objectifs

• Savoir coder la volatilité d’un actif
• Savoir calculer la variance et la variance mobile d’un actif
• Comprendre la notion de la volatilité
• Avoir l’importance de la volatilité
• Savoir calculer la volatilité de type sinusoïdal ou Gaussien
• Savoir la relation entre la volatilité et la valeur efficace
• Savoir différencier entre la volatilité globale et mobile
• Etc.

Comment calculer la volatilité ?

On utilise la variance (au bien l’écart-type (sigma) au carré) pour le calcul de la volatilité. Elle est analogue à la moyenne quadratique par rapport à la moyenne globale du prix (µ) (voir la première partie pour plus de détails). Elle permet de mesurer l’amplitude des variations autour de la moyenne globale. Ci-dessous la définition mathématique de la variance.

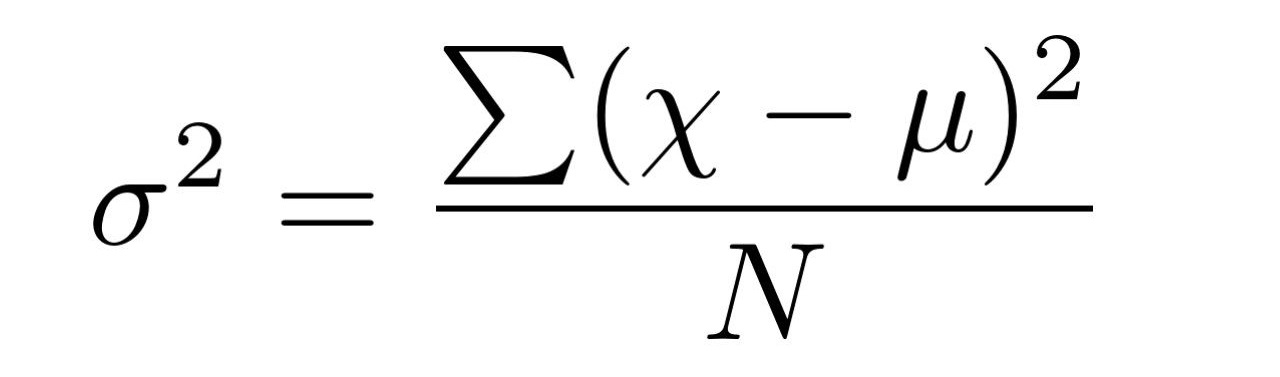
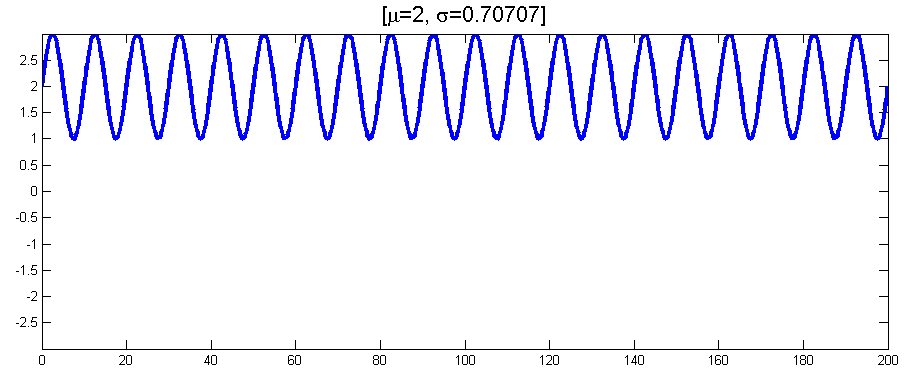
Volatilité sinusoïdale

La variance est équivalente à la valeur efficace dans le cas d’un signal sinusoïdal !

[pastacode lang=”c” manual=”%25%25%201.1%20Volatilit%C3%A9%20(sin)%20g(t)%3D%20A*sin(2*PI*f0*t)%0AN%3D1e4%3B%0At%3Dlinspace(0%2C200%2CN)%3B%20%25%20%5B0%2C200%5D%20Secondes%0AA%3D1%3B%0Aa0%3D2%3B%0At0%3D10%3B%20f0%3D1%2Ft0%3B%0Ap_t_s%3DA*sin(2*pi*f0*t)%2B%20a0%20%3B%0A%0A%25%20p_t_s%3Dp_t_s.*t%3B%20%25%20(%2B)%0A%25%20p_t_s%3Dp_t_s.*(max(t)-t)%3B%20%25%20(-)%20%0A%0A%25%25%201.3%20Prix%20p(t)%20%0Ap_t%3Dp_t_s%3B%0A%0A%25%25%202.%20Calcul%20de%20la%20valeur%20Moyenne%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20Somme%3DSomme%2Bp_t(i)%3B%0Aend%3B%0AMoy%3DSomme%2FN%3B%0A%0A%25%25%203.1%20Calcul%20de%20la%20Variance%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20pt1%3Dp_t(i)-Moy%3B%0A%20%20%20%20Somme%3DSomme%2Bpt1%5E2%3B%0Aend%3B%0AVar%3DSomme%2FN%3B%20%0A%25%20Var%3Dmean((p_t-mean(p_t)).%5E2)%3B%0A%25%20Var%3Dvar(p_t)%3B%0ASig%3Dsqrt(Var)%3B%0A%0A%25%25%20Affichage%20%0Afigure(1)%0Aplot(t%2Cp_t%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%20ylim(%5B-max(p_t)%20max(p_t)%5D)%3B%20%0Aset(gca%2C’color’%2C’none’)%3B%20hold%20on%3B%20%0Atitle(strcat(‘%5B%5Cmu%3D’%2Cnum2str(Moy)%2C’%2C%20%5Csigma%3D’%2Cnum2str(Sig)%2C%20’%5D’)%2C’fontsize’%2C16)%3B%0A%0A” message=”” highlight=”” provider=”manual”/]

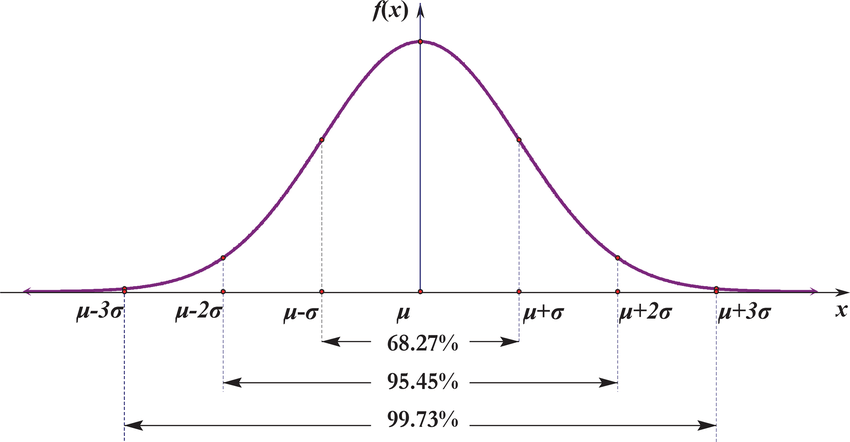
Volatilité gaussienne

Une fonction gaussienne est caractérisée par deux paramètres : la valeur moyenne (µ) et l’écart-type (Standard-déviation (std), racine carrée de la variance). L’écart-type (sigma). La probabilité d’apparition d’une valeur du prix dans le couloir définit par l’intervalle [µ-3*sigma, µ+3*sigma] est supérieure à 99% ! Ci-dessous un extrait du code pour la synthèse du bruit gaussien.

[pastacode lang=”c” manual=”sig%3D1%3B%0Amoy%3D0%3B%0Ap_t_g%3Dmoy%2Bsig*randn(1%2CN)%3B” message=”” highlight=”” provider=”manual”/]

Voir le tutoriel pour les détails techniques.

[pastacode lang=”c” manual=”%25%25%201.1%20Volatilit%C3%A9%20(sin)%20g(t)%3D%20A*sin(2*PI*f0*t)%0AN%3D1e4%3B%0At%3Dlinspace(0%2C200%2CN)%3B%20%25%20%5B0%2C200%5D%20Secondes%0AA%3D1%3B%0Aa0%3D2%3B%0At0%3D10%3B%20f0%3D1%2Ft0%3B%0Ap_t_s%3DA*sin(2*pi*f0*t)%2B%20a0%20%3B%0A%0A%25%20p_t_s%3Dp_t_s.*t%3B%20%25%20(%2B)%0A%25%20p_t_s%3Dp_t_s.*(max(t)-t)%3B%20%25%20(-)%20%0A%0A%25%25%201.2%20Volatilit%C3%A9%20de%20type%20Gaussien%20(Voir%20la%20suite)%0Asig%3D1%3B%0Amoy%3D10%3B%0Ap_t_g%3Dmoy%2Bsig*randn(1%2CN)%3B%0A%0A%0A%25%25%201.3%20Prix%20p(t)%20%0Ap_t%3Dp_t_g%3B%0A%0A%25%25%202.%20Calcul%20de%20la%20valeur%20Moyenne%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20Somme%3DSomme%2Bp_t(i)%3B%0Aend%3B%0AMoy%3DSomme%2FN%3B%0A%0A%25%25%203.1%20Calcul%20de%20la%20Variance%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20pt1%3Dp_t(i)-Moy%3B%0A%20%20%20%20Somme%3DSomme%2Bpt1%5E2%3B%0Aend%3B%0AVar%3DSomme%2FN%3B%20%0A%25%20Var%3Dmean((p_t-mean(p_t)).%5E2)%3B%0A%25%20Var%3Dvar(p_t)%3B%0ASig%3Dsqrt(Var)%3B%0A%0A%25%25%20Affichage%20%0Afigure(2)%0Asubplot(211)%3B%20plot(t%2Cp_t%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%20%0Aset(gca%2C’color’%2C’none’)%3B%0Atitle(strcat(‘%5B%5Cmu%3D’%2Cnum2str(Moy)%2C’%2C%20%5Csigma%3D’%2Cnum2str(Sig)%2C%20’%5D’)%2C’fontsize’%2C16)%3B%0A%0Asubplot(212)%3Bhist(p_t%2C300)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0Atitle(‘Distribution%20des%20valeurs’%2C’fontsize’%2C16)%3B%0A” message=”” highlight=”” provider=”manual”/]

Bruit gaussien pur

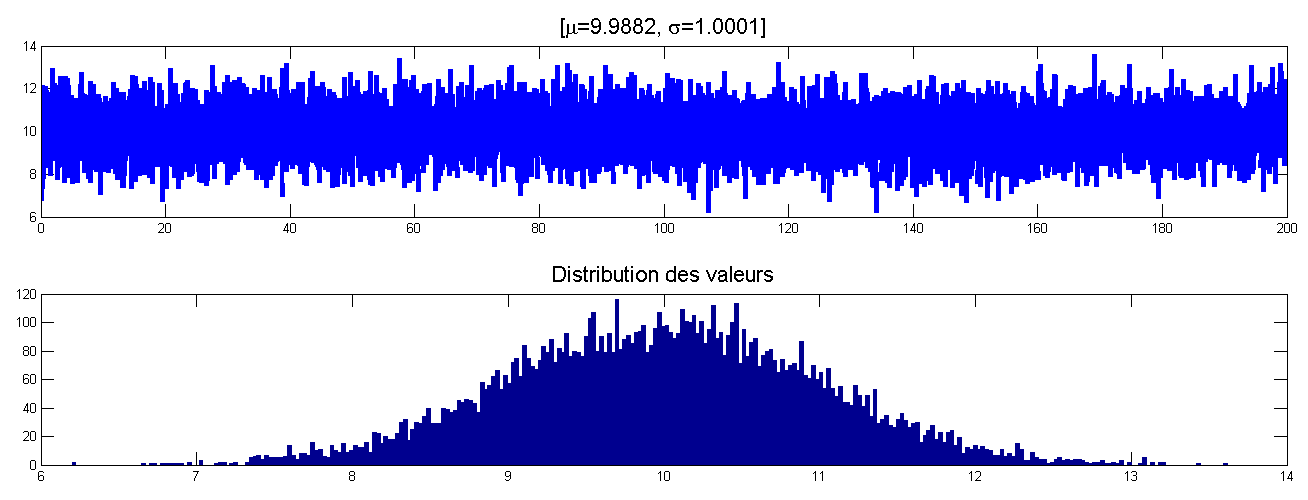
Sinus + bruit gaussien

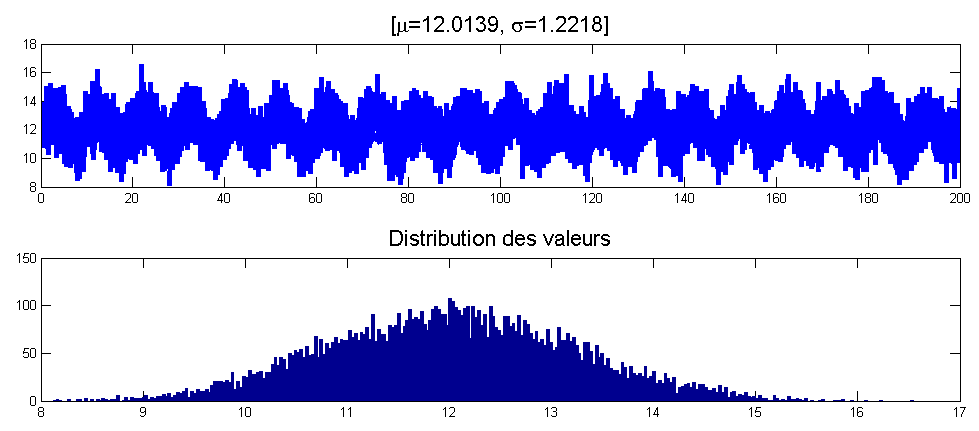
Sinus + faible bruit gaussien

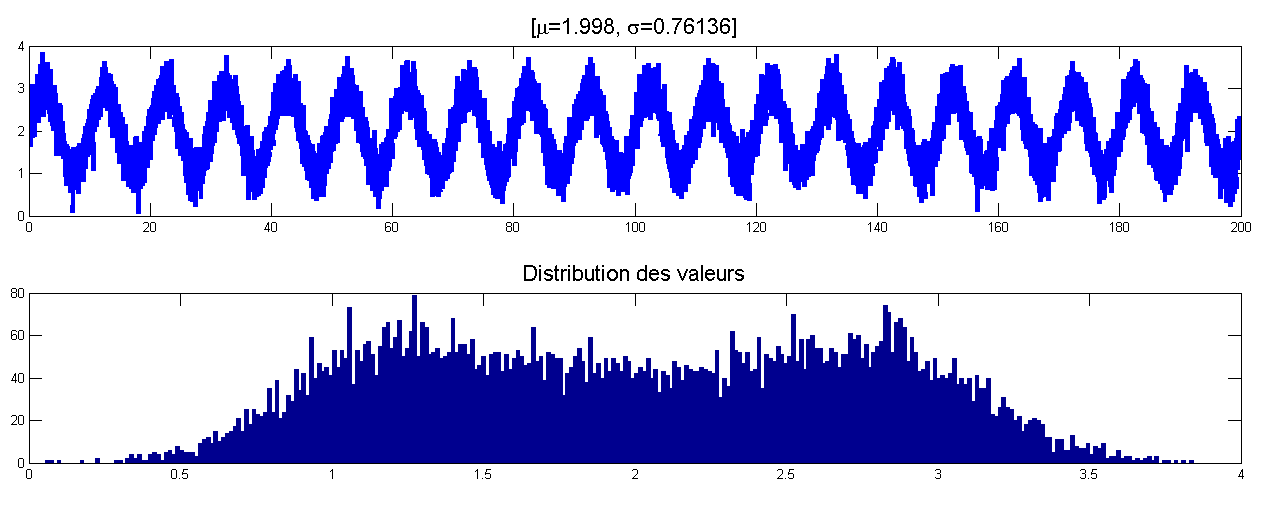
Calcul de la variance mobile (volatilité variable)

Principe

La variance mobile est utile lorsque l’amplitude des variations augment (ou  diminue) en fonction du temps, on parle des signaux son stationnaires. Dans ces conditions, il est préférable de calculer la variance mobile. Le calcul de la variance  mobile est analogue à celui de la moyenne mobile. On définit une fenêtre de taille M avec M<<N, N étant le nombre d’échantillons du signal. Le calcul consiste à recalculer la variance locale pour chaque M valeurs du plus anciennes aux plus récentes valeurs du signal. Ci-dessous la boucle de calcul de la variance mobile.

[pastacode lang=”c” manual=”VarM%3D0*p_t%3B%20%0AM%3D1000%3B%0Afor%20i%3DM%3AN%0A%20%20%20%20V%3Dp_t(i-M%2B1%3Ai)%3B%20%0A%20%20%20%20VarM(i)%3Dvar(V)%3B%0Aend%3B%0ASigM%3Dsqrt(VarM)%3B%20″ message=”” highlight=”” provider=”manual”/]

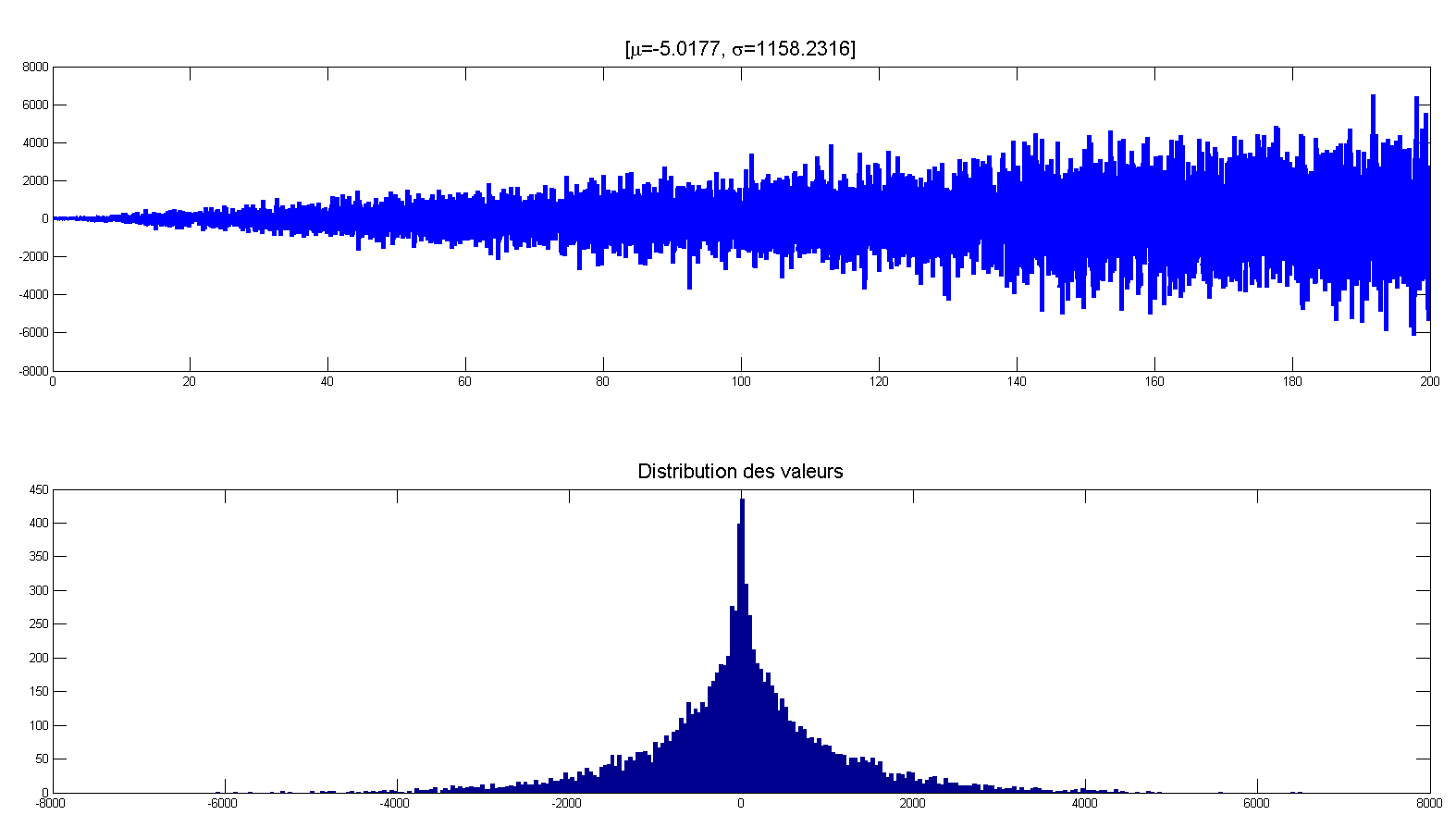
Exemple: Bruit gaussien

L’exemple simule un bruit gaussien avec une variance mobile linéairement en fonction du temps. Le bruit b(t) est définit par une distribution gaussienne g(t) multipliée par la variable (t) : b(t) =g(t)*t afin d’avoir une croissance linéaire de l’amplitude en fonction du temps. Ci-dessous l’extrait du code de la synthèse et le calcul de la variance mobile.

[pastacode lang=”c” manual=”%25%25%201.1%20Volatilit%C3%A9%20(sin)%20g(t)%3D%20A*sin(2*PI*f0*t)%0AN%3D1e4%3B%0At%3Dlinspace(0%2C200%2CN)%3B%20%25%20%5B0%2C200%5D%20Secondes%0AA%3D1%3B%0Aa0%3D0%3B%0At0%3D5%3B%20f0%3D1%2Ft0%3B%0Ap_t_s%3DA*sin(2*pi*f0*t)%2B%20a0%20%3B%0Ap_t_s%3Dp_t_s.*(max(t)-t)%3B%0A%0A%25%25%201.2%20Volatilit%C3%A9%20de%20type%20Gaussien%20(Voir%20la%20suite)%0Asig%3D10%3B%0Amoy%3D0%3B%0Ap_t_g%3Dmoy%2Bsig*randn(1%2CN)%3B%0A%0A%0A%25%25%20Prix%20p(t)%20%0Ap_t%3Dt.*p_t_g%3B%0A%0A%25%25%202.%20Calcul%20de%20la%20valeur%20Moyenne%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20Somme%3DSomme%2Bp_t(i)%3B%0Aend%3B%0AMoy%3DSomme%2FN%3B%0A%0A%25%25%203.1%20Calcul%20de%20la%20Variance%20%0ASomme%3D0.0%3B%0Afor%20i%3D1%3AN%0A%20%20%20%20pt1%3Dp_t(i)-Moy%3B%0A%20%20%20%20Somme%3DSomme%2Bpt1%5E2%3B%0Aend%3B%0AVar%3DSomme%2FN%3B%20%0A%25%20Var%3Dmean((p_t-mean(p_t)).%5E2)%3B%0A%25%20Var%3Dvar(p_t)%3B%0ASig%3Dsqrt(Var)%3B%0A%0A%25%25%203.1%20Calcul%20de%20la%20Variance%20Mobile%20%0AVarM%3D0*p_t%3B%20%0AM%3D1000%3B%0Afor%20i%3DM%3AN%0A%20%20%20%20V%3Dp_t(i-M%2B1%3Ai)%3B%20%0A%20%20%20%20VarM(i)%3Dvar(V)%3B%0Aend%3B%0ASigM%3Dsqrt(VarM)%3B%20%0A%0A%25%25%204.%20Affichage%20%0Afigure(1)%0Aplot(t%2Cp_t%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%20ylim(%5B-max(p_t)%20max(p_t)%5D)%3B%20%0Aset(gca%2C’color’%2C’none’)%3B%20hold%20on%3B%20%0Aplot(t%2CSigM%2C’r’%2C%20’linewidth’%2C3)%0Atitle(strcat(‘%5B%5Cmu%3D’%2Cnum2str(Moy)%2C’%2C%20%5Csigma%3D’%2Cnum2str(Sig)%2C%20’%5D’)%2C’fontsize’%2C16)%3B%0Apause%20(0.5)%3B%20%0A%0Afigure(2)%0Asubplot(211)%3B%20plot(t%2Cp_t%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%20%0Aset(gca%2C’color’%2C’none’)%3B%0Atitle(strcat(‘%5B%5Cmu%3D’%2Cnum2str(Moy)%2C’%2C%20%5Csigma%3D’%2Cnum2str(Sig)%2C%20’%5D’)%2C’fontsize’%2C16)%3B%0Asubplot(212)%3Bhist(p_t%2C300)%3B%0Aset(gca%2C’color’%2C’none’)%3B%0Atitle(‘Distribution%20des%20valeurs’%2C’fontsize’%2C16)%3B%0A” message=”” highlight=”” provider=”manual”/]

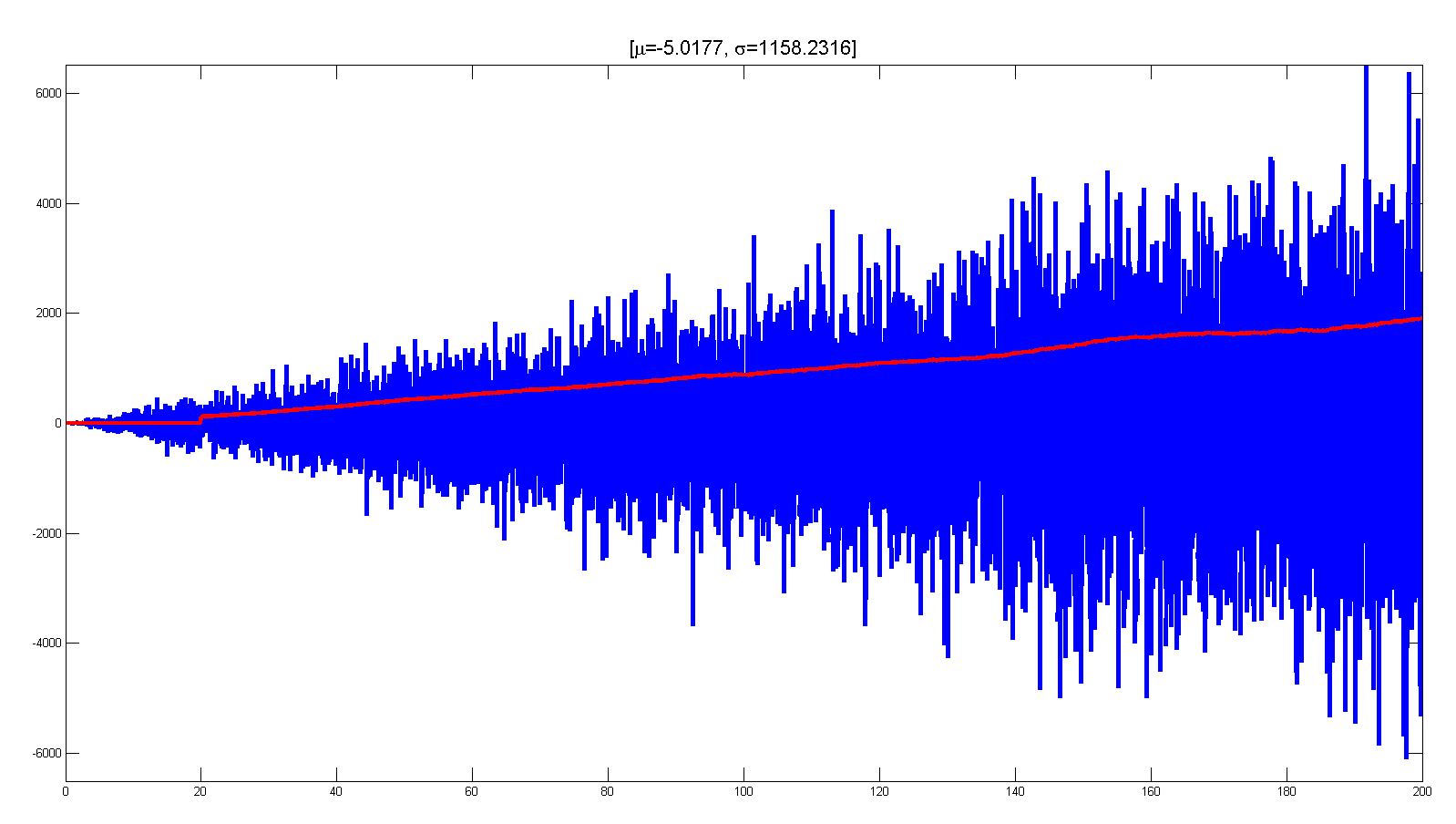
On verra dans le tutoriel prochain une analyse comparative de la volatilité de quelques indices majeurs (CAC 40, S&P 500, etc.).