Objectifs

• Comprendre la notion de la tendance
• Introduire la notion de la volatilité
• Savoir modéliser avec Matlab la tendance avec des approximation linéaires
• Se familiariser avec la notion des cycles, fréquences, etc.
• Savoir la relation entre la tendance et la dérivée première
• Savoir détecter la tendance d’un actif
• Etc.

Modèle linéaire de la tendance

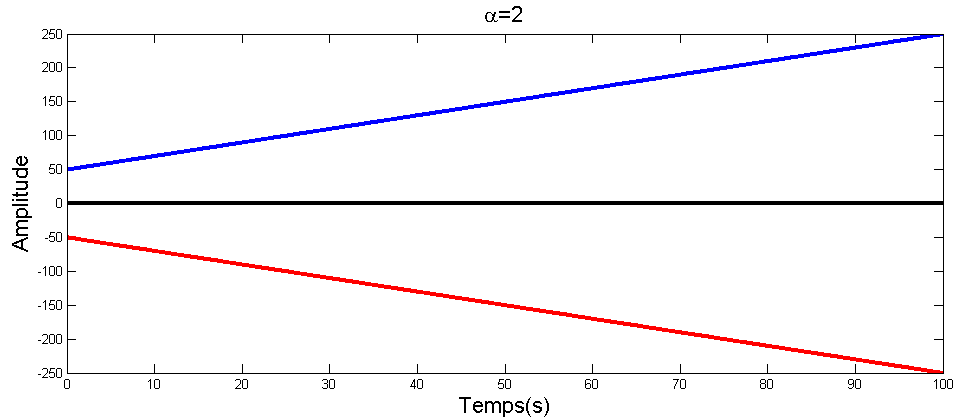
Le modèle linéaire de la tendance consiste à approximer la tendance d’un actif d’une façon locale ou globale avec une droite. On a l’habitude de tracer des  droites de tendances manuellement durant l’analyse technique, mais on réalité on fait des approximations linéaires de la tendance  J . Une droite elle est définie par deux paramètres : la pente de la droite (ou la tangente, variable (a) ), elle indique le sens de la droite (vers le bas ou vers le haut) ainsi la vitesse de croissance de la droite. Une pente très raide indique une croissance rapide du prix,  en revanche une pente tant vers zéro montre une variation lente du prix de l’actif. Le deuxième paramètre est l’offset (ou le décalage, variable (b)) de la droite, elle définit le point de départ de la droite. On peut définir la fonction f(t) de la tendance de la façon suivante : f(t)=a*t+b. Le signe de (a) indique la nature de la tendance : tendance haussière (signe positif), tendance baissière (signe négative), range ((a) tant vers zéro).

[pastacode lang=”c” manual=”%25%25%201.%20Tendance%3A%20f(t)%20%3D%20a*t%20%2B%20b%20%3B%20f(t)%20%3D%20-a*t%20%2B%20b%0AN%3D1e3%3B%0At%3Dlinspace(0%2C100%2CN)%3B%20%25%20%5B0%2C100%5D%20Secondes%0Aa%3D2%3B%0Ab%3D50%3B%0An%3D1%3B%0Af_t_h%3Da*t.%5En%2Bb%3B%0Af_t_b%3D-a*t.%5En-b%3B%0A%0Afigure(1)%3B%0Aplot(t%2Cf_t_h%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%20hold%20on%3B%0Aplot(t%2Cf_t_b%2C’r’%2C%20’linewidth’%2C3)%3B%20xlabel(‘Temps(s)’%2C’fontsize’%2C16)%3B%20ylabel(‘Amplitude’%2C’fontsize’%2C16)%3B%0Aplot(t%2Czeros(1%2Clength(f_t_h))%2C’k’%2C%20’linewidth’%2C3)%3Bhold%20off%3B%0Aset(gca%2C%20’color’%2C%20’none’)%3B%20hold%20on%3B%0Atitle(strcat(‘%5Calpha%3D’%2Cnum2str(a))%2C’fontsize’%2C16)%3B%0A” message=”” highlight=”” provider=”manual”/]

Modèle sinusoïdal de la volatilité

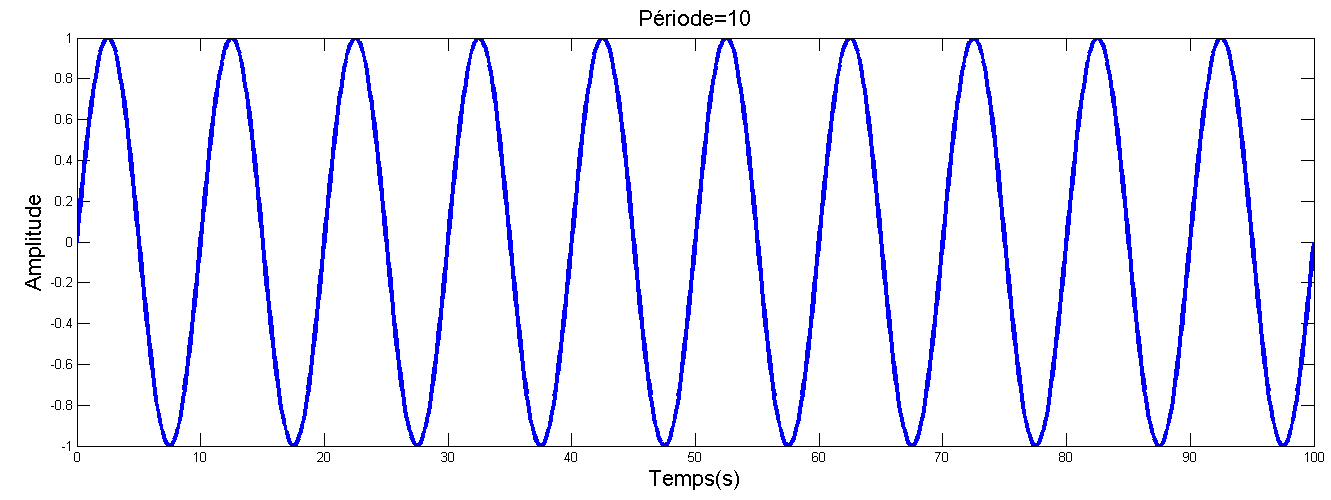
Un actif en bourse est définit pas sa tendance ainsi sa volatilité. La volatilité montre les fluctuations du prix autour de la tendance. Dans le tutoriel on abordera une volatilité de type sinusoïdal pour des raisons de simplifications. On verra dans la suite le modèle générique de la volatilité. Une fonction sinusoïdal est définit par son amplitude et sa fréquence (inverse de la période en seconde). La fonction sinusoïdal est l’atome de l’analyse harmonique (ou fréquentielle) d’un actif. Elle permet de mieux comprendre la notion des cycles, fréquences, etc. Elle nous sera de grande utilité dans la suite de la série. De plus le phénomène des cycles et très présent dans les marchées financiers. La fonction sinusoïdale g(t) est définit par : g(t)=A*sin(2*PI*f0*t). (A) est l’amplitude, (f0) est la fréquence (voir le tutoriel pour plus de détails).

[pastacode lang=”c” manual=”%25%25%202.%20Volatilit%C3%A9%3A%20g(t)%3D%20A*sin(2*PI*f0*t)%0A%0AA%3D1%3B%0At0%3D10%3B%20f0%3D1%2Ft0%3B%0Ag_t%3DA*sin(2*pi*f0*t)%3B%0A%0Afigure(1)%3B%0Aplot(t%2Cg_t%2C%20’linewidth’%2C3)%3Bxlim(%5Bt(1)%20t(end)%5D)%3B%0Aset(gca%2C%20’color’%2C%20’none’)%3Bxlabel(‘Temps(s)’%2C’fontsize’%2C16)%3B%0Aylabel(‘Amplitude’%2C’fontsize’%2C16)%3B%0Atitle(strcat(‘P%C3%A9riode%3D’%2Cnum2str(t0))%2C’fontsize’%2C16)%3B%0A” message=”” highlight=”” provider=”manual”/]

Modèle du prix p(t)

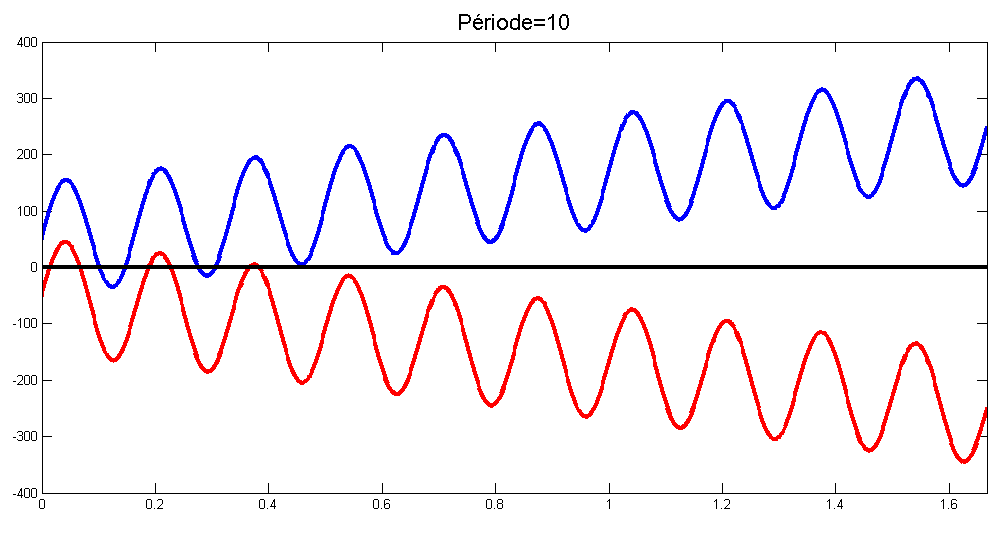
Le prix p(t) peut être décrit par une combinaison linaire de la tendance f(t) et la volatilité g(t) : p(t)=f(t)+g(t).

Programme complet

[pastacode lang=”c” manual=”clc%3B%20close%20all%3B%20clear%20all%3B%0A%0A%0A%25%25%20Ing%C3%A9nierie%20%26%20Bourse%0A%25%25%20Ingenierie-Bourse.fr%0A%25%25%20Tendance%3A%20Partie%202%2F2%0A%0A%25%25%201.%20Tendance%3A%20f(t)%20%3D%20a*t%20%2B%20b%20%3B%20f(t)%20%3D%20-a*t%20%2B%20b%0AN%3D1e3%3B%0At%3Dlinspace(0%2C100%2CN)%3B%20%25%20%5B0%2C100%5D%20Secondes%0Aa%3D2%3B%0Ab%3D50%3B%0An%3D1%3B%0Af_t_h%3Da*t.%5En%2Bb%3B%0Af_t_b%3D-a*t.%5En-b%3B%0A%0A%25%25%202.%20Volatilit%C3%A9%3A%20g(t)%3D%20A*sin(2*PI*f0*t)%0A%0AA%3D100%3B%0At0%3D10%3B%20f0%3D1%2Ft0%3B%0Ag_t%3DA*sin(2*pi*f0*t)%3B%0A%0A%25%25%203.%20Prix%3A%20p(t)%0Ap_t_h%3Df_t_h%2Bg_t%3B%0Ap_t_b%3Df_t_b%2Bg_t%3B%0A%0A%25%25%20Affichage%0Afigure(1)%3B%0Atm%3Dt%2F60%3B%0Aplot(tm%2Cp_t_h%2C%20’linewidth’%2C3)%3Bxlim(%5Btm(1)%20tm(end)%5D)%3B%20hold%20on%3B%0Aplot(tm%2Cp_t_b%2C’r’%2C%20’linewidth’%2C3)%3B%0Aplot(tm%2Czeros(1%2Clength(p_t_h))%2C’k’%2C%20’linewidth’%2C3)%3Bhold%20off%3B%0Aset(gca%2C’color’%2C’none’)%3B%0Atitle(strcat(‘P%C3%A9riode%3D’%2Cnum2str(t0))%2C’fontsize’%2C16)%3B%0Apause(0.1)%3B%0A” message=”” highlight=”” provider=”manual”/]